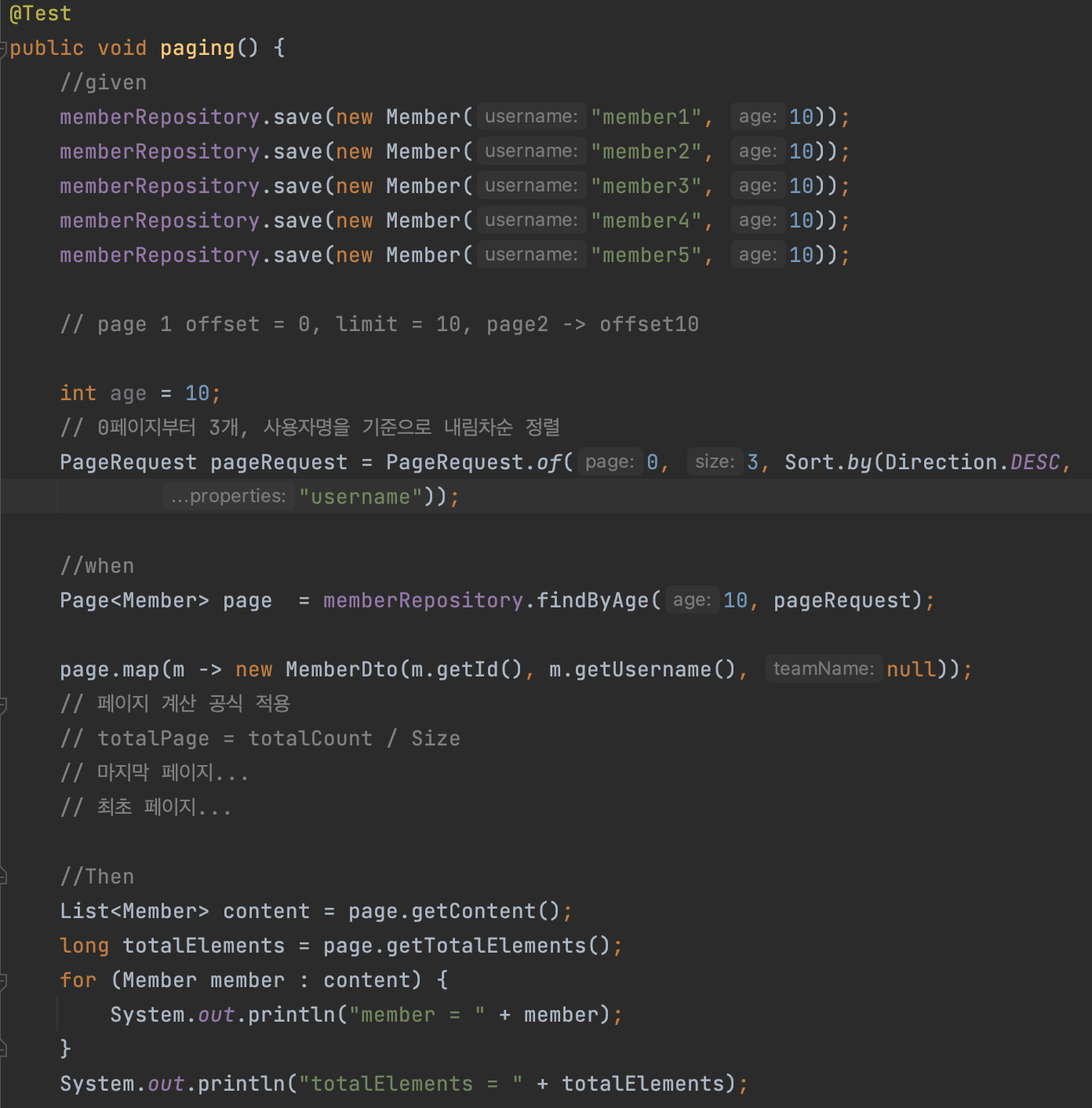
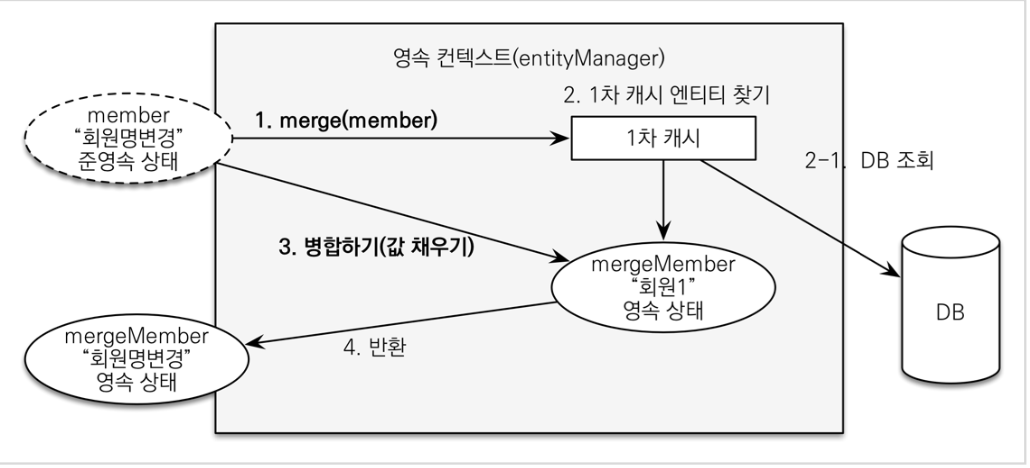
인터넷 통신에서 클라이언트와 서버는 어떻게 통신할까요? 클라이언트 컴퓨터와 서버 컴퓨터 사이에 인터넷이라는 것이 존재합니다. 이 복잡한 인터넷 망은 수많은 노드들로 구성되어 있습니다. 그래서 이러한 복잡한 망을 처리하기 위해 각각의 컴퓨터에 IP(Internet Protocol) 주소라는 것을 부여했습니다. IP프로토콜을 통해 다음과 같이, 클라이언트와 서버는 각각의 IP주소를 통해 Packet 단위로 데이터를 전달할 수 있게 됩니다. IP 패킷은 S.A IP(출발지 IP), D.A IP(목적지 IP), 전송 데이터로 구성되어 있으며, 클라이언트에서 이 패킷을 전송할 때, 수많은 노드들을 거쳐 서버로 전송됩니다. 또한 같은 맥락으로 서버도 잘 받았다는 응답 패킷을 클라이언트로 전송하게 됩니다. 하지만 I..